Chapter 1 - Atoms Chapter 2 - Gases Chapter 3 - Ions Chapter 4 - Salts Chapter 5 - MD

Noble Gases

The Ideal Gas Law

The ideal gas law is an empirical law; it's a relationship between the pressure in a system of gases to the volume, the temperature, and the number of gas atoms/molecules in the system. This "law" is valid if the gas atoms/molecules are infinitely small and do not interact (ideal), but real gases are not ideal (even noble gases have attraction and volume). Nonetheless the ideal gas laws and equations do an excellent job of describing the behaviors of gases (particularly the noble gases). The ideal gas law was developed by combining sets of famous more simple gas laws that were each established through clever experiments. Each of these gas laws is named after the scientist who discovered it, and these laws were all discovered long before the invention of computers. Mathematically, the ideal gas law is given by the following equation:

PV=NK_bT

This equation shows that the product of the pressure (P) and the volume (V) is directly proportional to the product of the number of atoms (N) and the absolute temperature (T) — the constant of proportionality in this version of the ideal gas equation is K_b.

The ideal gas law suggests a number of important relationships.

At constant temperature and volume, the pressure is linearly proportional to the number of atoms in the container.
For a fixed volume of gas in a closed container, the pressure is linearly proportional to the temperature.
At constant temperature and pressure, the volume is linearly proportional to the number of atoms in the container.
For a fixed amount gas (N=constant) in a flexible container at constant pressure, the volume of the container must expand or contract in direct proportion to the temperature.
At a constant temperature with a fixed number of atoms, the volume is inversely proportional to the pressure (i.e. in order to double the pressure you must halve the volume).

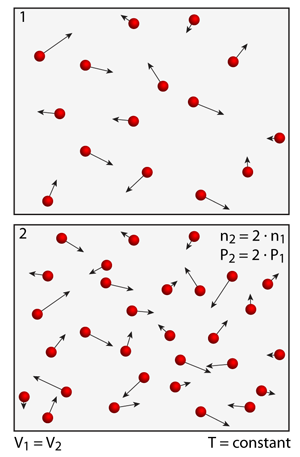
A simple experiment that you can try is to measure the pressure as you add or remove atoms from the simulation; it is important to maintain a constant volume in the simulation when you do this experiment. Notice the simple and linear relationship — if you double the number of atoms in the simulation the pressure also doubles.

The scientists that gave us the original gas laws were only able to perform experiments on fixed systems of gases — in their experiments the number of gas molecules was always constant. Using this atomistic simulation you can actually perform a number of simple experiments that they could not. For example, what happens to the pressure in the system as you increase the number of atoms?

Pressure vs. Number of Atoms

In addition to the pressure being dependent on the momentum change that occurs at wall collisions, the pressure also depends on the number of collisions per unit time. If the temperature is maintained constant then the average impulse forces that arise from collisions is also constant (for a given atom type). Thus, under conditions of constant temperature and volume the number of atomistic collisions with the walls increases or decreases in direct proportion to the number of atoms in the simulation. This relationship will hold as long as the temperature is maintained constant and there are not too many atoms in the simulation. Simply put, if you increase the number of atoms in the simulation then you increase the number of collisions, and this increase in the number of collisions results in an increase in the pressure.

Now try and perform your experiments at different temperatures — notice that this effect is independent of the absolute temperature (doubling the number of atoms in the simulation always doubles the pressure).

While you're doing these experiments, add and remove different noble gases from the simulation. You may be surprised to find that the pressure is the same whether there are 50 helium atoms or 50 krypton atoms in the simulation. Notice that the heavier Krypton atoms collide with the surfaces less frequently; however, this decrease in collision frequency is balance by a proportional increase in their momentum.

Deviations to the ideal gas law can be observed when the simulation becomes over packed with atoms. In the ideal gas laws the atoms are assumed to occupy no volume, but in reality all atoms have a finite size. As the simulation becomes very dense the pressure begins to increase non-linearly. This is due to increases in collision frequency that arises because the extra atoms are occupying a large percentage of the volume within the container.

Pressure vs. Temperature: "Gay-Lussac's Law" and "Charles's Law"

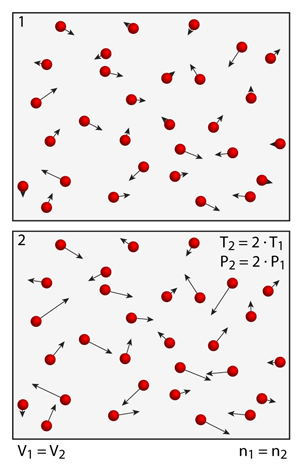
Gay-Lussac found that the pressure increased linearly with temperature when he performed experiments using a fixed container of gases. You can try this experiment by gradually increasing or decreasing the temperature in the simulation and observe the changes in pressure as you add or remove energy.

Gay-Lussac found that the pressure of a closed system of gases increased when the temperature was increased, and Charles found that if the pressure was held constant the volume of the system increased as the temperature was increased. Why does pressure increase linearly with increasing temperature? And if the pressure is constant, why do gases expand as their temperature rises?

You can perform a number of experiments to explore these laws. Take a system of 50 helium atoms in a volume that is large enough that they can travel at least 10 or more diameters between collisions — now change the temperature. As you increase the temperature in the simulation, the atoms move faster. Recall that temperature is related to the square of the speed; thus, you have to increase the temperature in the simulation by a factor of 4x (from 100K to 400K for example) in order to double the average speed of the atoms. In a closed system, such as the above 50 helium atom simulation, if the average speed of the atoms is doubled their collisions with the boundaries will occur twice as frequently. The more frequent the collisions the higher the pressure, but notice that the pressure is more than doubled. Why?

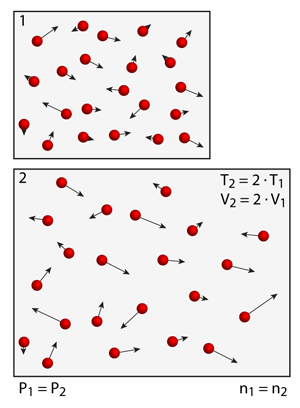
Charles observed that under conditions where the pressure of the container was maintained constant, any changes in temperature resulted in a linearly proportional change in the container volume. This is a challenging experiment for you to try with the simulation. If you increase the temperature in the simulation then you'll notice an increase in pressure. In order to get the pressure back to the original pressure you must expand the volume of simulation.

You can change the volume of the simulation boundaries by pinching or expanding your fingers (zooming in and out of the simulation).

The answer lies in momentum. Because the atoms are moving faster their momentum is greater — momentum is a product of the atomic mass and the velocity. When you increased the temperature by a factor of four (4x), you increased the velocity and the momentum of the atoms by a factor of two (2x); this doubling of the momentum doubles the impulsive forces that occurs at each collision.

Take these two effects that occurred as a result of your increasing the temperature in the system and look at the combined effect of these changes on pressure. If you increase the temperature by a factor of four, then the atoms are colliding twice as frequently and with twice the momentum. As discussed earlier, pressure is a function of both the number of collisions (2x) and the change in momentum of each collision (2x); thus, an increase in the temperature by a factor of four increases the pressure by a factor a four (2x2=4)! The relationship between temperature and pressure is linear. Increasing or decreasing the temperature has an immediate and proportional effect on the pressure.

Deviations for this ideal gas behavior are evident at low temperatures. In these simulations, the temperatures can be reduced to levels that cause the noble gases to condense. As these atoms condense, the collision frequencies are no longer linearly proportional to the average velocity. Notice some of the unique behavior of atomic pairs that rotate like "dumb-bells" as they travel across the simulation. Additionally, large nearly stationary clumps of atoms can form in the interior of the simulation — these clusters of atoms still have significant kinetic energy but no longer collide with the boundaries. This deviation is expected, the ideal gas law assumes that the gas particles do not interact (an assumption that is valid when the temperatures are well above the condensation temperatures).

Pressure vs. Volume: "Boyle's Law"

If the number of atoms is fixed and the temperature is held constant then there is a very unique relationship between the pressure and the volume. Boyle was the first to notice that the product of the pressure and the volume was a constant. In order to test this within the simulation try to expand or compress the volume and watch what happens to the pressure. In order to change the volume in the simulation, use your fingers to "pinch" or "zoom"; the atoms appear larger or smaller depending on the scale — the atoms look larger when the volume is smaller.

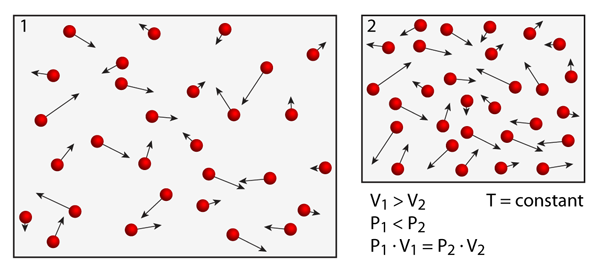
For a closed system at constant temperature the pressure is inversely proportional to the volume. Thus, if you double the volume the pressure drops by half. Notice that as you decrease the volume the atoms collide more frequently with the boundaries. Deviations from ideality will occur if the simulation volume becomes too small or the density of atoms becomes too great.

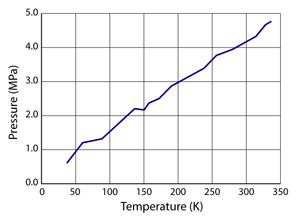
Dynamic Graphing: Pressure vs. Temperature, Volume, or the Number of Atoms

In these simulations the pressure is continuously being measured and saved as a function of the current state of the simulation. To access the dynamic graphs tap the graph button on the top right of the simulation (tap again to hide the graph). Under conditions where only one parameter is changing the graph will dynamically display the pressure values as a function of the changing parameter. The x–axis will automatically switch to display the parameter that changed.

When changing the temperature of the system the graph will dynamically display the pressure as a function of the current and past temperatures. The graph clears if there are any changes to the volume or the number of atoms in the simulation.